This post is about superconduiting qubits or similar devices discussed in work I published during graduate school [P. Li, P.M. Wu, Y. Bomze, I.V. Borzenets, G. Finkelstein, A.M. Chang, Phys. Rev. Lett. 107, 137004 (2011) and P. Li, P.M. Wu, Y. Bomze, I.V. Borzenets, G. Finkelstein, A.M. Chang Phys. Rev. B 84, 184508 (2011)].
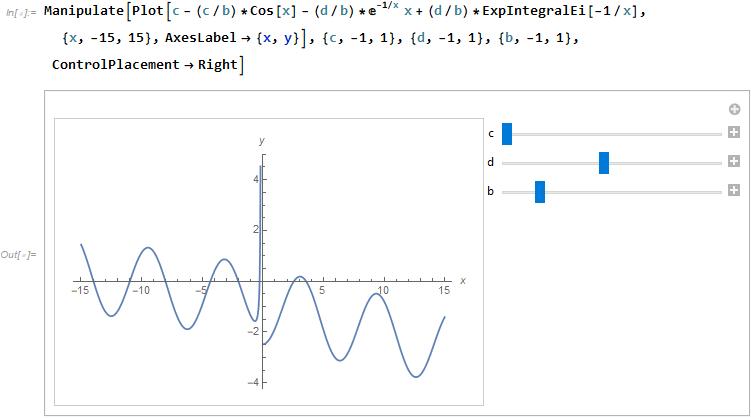
The way I remember thinking about Josephson junctions (or superconducting phase slip devices) is with the resistor-capacitor-superconducting junction (RCSJ) model. Basically, take a RLC circuit and replace or modify the inductor with a superconducting junction that has its own well defined current and voltage condition. The figure below outlines this circuit and the superconducting junction with phase \theta (related to the voltage) and current I, related to the phase.
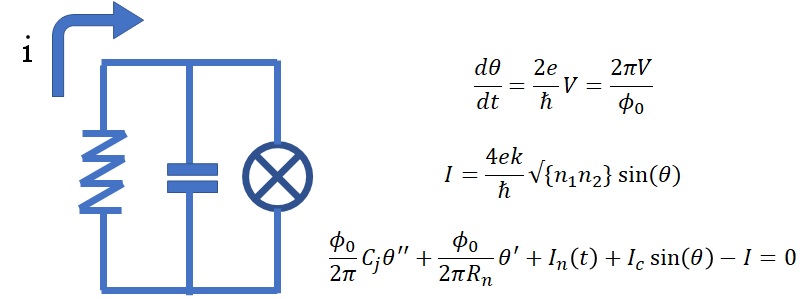
RCSJ circuits can be solved by considering the current flowing through all the elements. Depending on the initial conditions, one can solve (see the image of the Mathematica notebook above) the 2nd order differential equation and get what looks like a “tilted” washboard potential. Electrons, coupled, either rise or slide through the potential crest and troughs, or in some weird cases, may tunnel through a wave barrier. Our work was looking for tunnel events, which are typically rare, and in the laboratory show up only at low temperatures (in the milliKelvins).
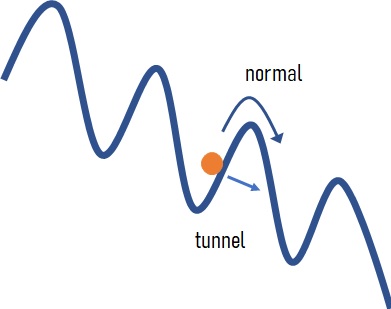
These rare tunnel events are actually important indicators of the material properties and robustness of the superconducting junction. Each time the particle moves into another wave trough, the phase “slips” so that the entire superconducting junction loses its coherence. How the slip occurs, either normally (by increasing voltage or current to tilt the slope of the washboard), or by tunneling is what we were fundamentally trying to understand. To tunnel the particle has to be found in an energetically favorable situation.
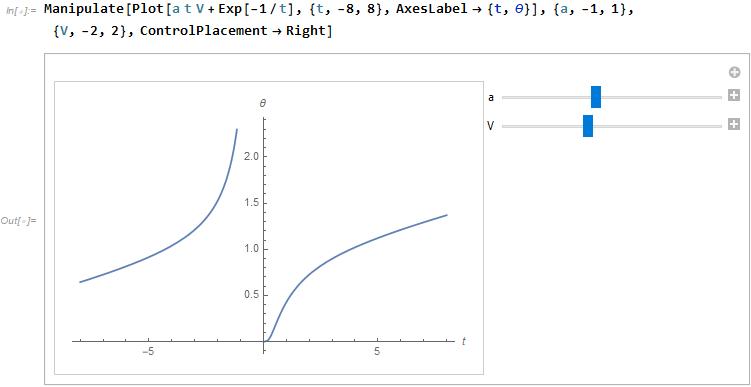
From the set of equations in the circuit figure above, it’s also possible to develop intuition for the current-voltage (IV) characteristics of the junction. Quantum devices can be made from such “nanowires” and the IV curves can be extracted and plotted. Here I make a crude plot of how the IV might look like (ignore negative “\theta”).
Interestingly enough, I make science fiction aside here to ponder the question whether the many worlds theory would be applicable here. One could argue that the particles carry over phase information from a prior wave trough before slippage in the new wave trough via it’s momentum, energetics and position. In a tunneling event however, the particle accesses “the void”. What information is then conveyed from going there?!